Trigonometry Formulas list - For all the trigonometry ratios

Here are some Trigonometry Formulas list - For all the trigonometry ratios , you will find this useful in your exams and in competitive exams.


The general trigonometry ratios for a right-angled triangle can be written as;

sinθ = OppositesideHypotenuse

cosθ = AdjacentSideHypotenuse

tanθ = OppositesideAdjacentSide

secθ = HypotenuseAdjacentside

cosecθ = HypotenuseOppositeside

cotθ = AdjacentsideSideopposite

Similarly, for a unit circle, for which radius is 1, and θ is the angle.Then,

sinθ = y/1

cosθ = 1/y

tanθ = y/x

cotθ = x/y

secθ = 1/x

cosecθ = 1/y

Trigonometry Identities and Formulas

Tangent and Cotangent Identities

tanθ = sinθcosθ

cotθ = cosθsinθ

Reciprocal Identities

sinθ = 1/cosecθ

cosecθ = 1/sinθ

cosθ = 1/secθ

secθ = 1/cosθ

tanθ = 1/cotθ

cotθ = 1/tanθ

Pythagorean Identities

sin2θ + cos2θ = 1

1 + tan2θ = sec2θ

1 + cot2θ = cosec2θ

Even and Odd Formulas

sin(-θ) = -sinθ

cos(-θ) = cosθ

tan(-θ) = -tanθ

cot(-θ) = -cotθ

sec(-θ) = secθ

cosec(-θ) = -cosecθ

Cofunction Formulas

sin(900-θ) = cosθ

cos(900-θ) = sinθ

tan(900-θ) = cotθ

cot(900-θ) = tanθ

sec(900-θ) = cosecθ

cosec(900-θ) = secθ

Formulas for twice of angle

sin2θ = 2 sinθ cosθ

cos2θ = 1 – 2sin2θ

tan2θ = 2tanθ1−tan2θ

Half Angle Formulas

sinθ = ±1−cos2θ2−−−−−−√

cosθ = ±1+cos2θ2−−−−−−√

tanθ = ±1−cos2θ1+cos2θ−−−−−−√

Formulas for Thrice of angle

sin3θ = 3sinθ – 4 sin3θ

Cos 3θ = 4cos3θ – 3 cosθ

Tan 3θ = 3tanθ–tan3θ1−3tan2θ

Cot 3θ = cot3θ–3cotθ3cot2θ−1

The Sum and Difference Formulas

Sin (A+B) = Sin A Cos B + Cos A Sin B

Sin (A-B) = Sin A Cos B – Cos A Sin B

Cos (A+B) = Cos A Cos B – Sin A Sin B

Cos (A-B) = Cos A Cos B + Sin A Sin B

Tan (A+B) = TanA+TanB1–TanATanB

Tan (A-B) = TanA–TanB1+TanATanB

The Product to Sum Formulas

Sin A Sin B = ½ [Cos (A-B) – Cos (A+B)]

Cos A Cos B = ½ [Cos (A-B) + Cos (A+B)]

Sin A Cos B = ½ [Sin (A+B) + Sin (A+B)]

Cos A Sin B = ½ [Sin (A+B) – Sin (A-B)]

The Sum to Product Formulas

Sin A + Sin B = 2 sin A+B2 cos A−B2

Sin A – Sin B = 2 cosA+B2 sin A−B2

Cos A + Cos B = 2 cosA+B2 cos A−B2

Cos A – Cos B = – 2 sinA+B2 sin A−B2

Inverse Trigonometric Functions

If Sin θ = x, then θ = sin-1 x = arcsin(x)

Similarly,

θ = cos-1x = arccos(x)

θ = tan-1 x = arctan(x)

Also, the inverse properties could be defined as;

sin-1(sin θ) = θ

cos-1(cos θ) = θ

tan-1(tan θ) = θ

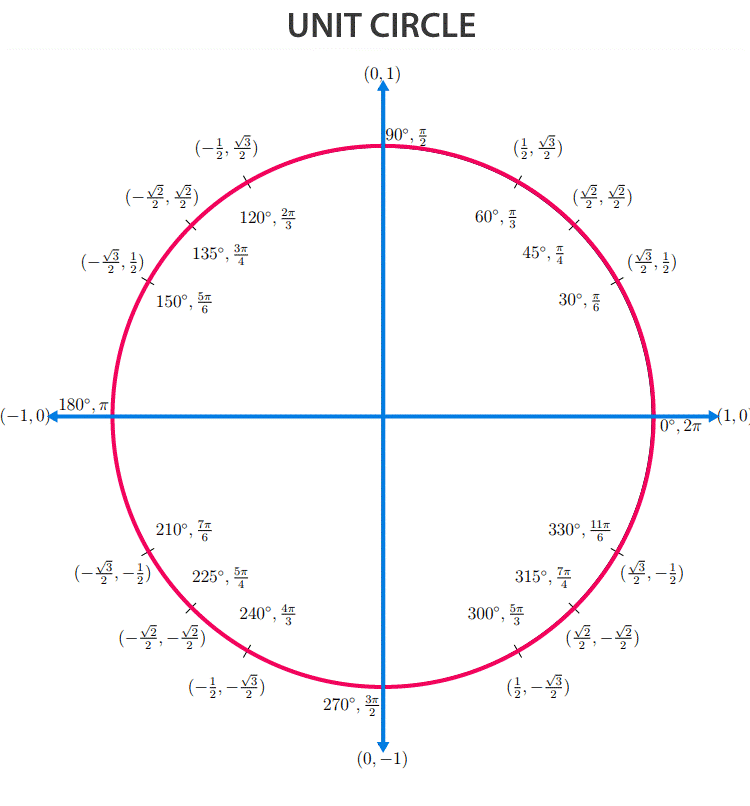
Values for Trigonometry ratios:

Degrees	00	300	450	600	900	1800	2700	3600
Radians	0	π/6	π/4	π/3	π/2	π	3π/2	2π
Sinθ	0	1/2	1/2–√	3–√/2	1	0	-1	0
Cosθ	1	3–√/2	1/2–√	1/2	0	-1	0	1
Tanθ	0	1/3–√	1	3–√	∞	0	∞	0
Cotθ	∞	/3–√	1	1/3–√	0	∞	0	∞
Secθ	1	2/3–√	/2–√	2	∞	-1	∞	1
Cosecθ	∞	2	/2–√	2/3–√	1	∞	-1	∞